链表(linked list)
链表的特点是元素可以存储到内存的任意位置,每个元素都通过指针变量存储下一个元素的地址,从而将元素串接起来形成的,因此每个单元至少有两个域。
一、单链表(single linked list)
一个域用于数据元素的存储,另一个域是指向其他单元的指针。
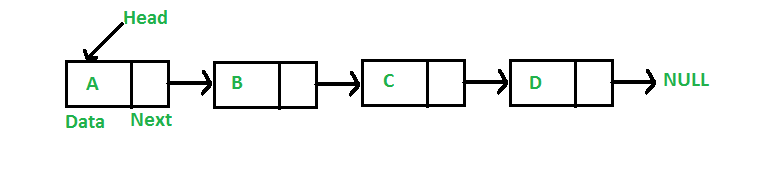
这里具有一个数据域和多个指针域的存储单元通常称为结点(node)一种最简单的结点结构如图所示,它是构成单链表的基本结点结构。在结点中数据域用来存储数据元素,指针域用于指向下一个具有相同结构的结点。
因为只有一个指针结点,称为单链表。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 | /**************************************************************** * 描述: 单链表的C++实现 * 作者: Alex Li * 日期: 2022-04-18 20:05:00 * 最后编辑时间: 2024-04-16 12:26:31 ****************************************************************/ #include <iostream> using namespace std; int n; // 全局变量n,用于存储节点数量 // 链表节点结构的定义 struct Node{ int data; // 节点的数据元素 Node *next; // 指向下一个节点的指针 }; Node *head = NULL; // 链表的头指针,初始设置为NULL // 函数原型声明,便于清晰和组织 void PrintNode(); // 向链表中添加节点的函数 void AddNode(){ cout << "请输入节点的数量: "; cin >> n; // 输入节点数量 Node *newNode = new Node; // 在内存中分配一个新节点 head = newNode; // 将头指针设置为新节点 cout << "请输入节点的数据: "; int x; // 临时变量x,用于存储节点数据 for (int i = 0; i < n; i++) { cin >> x; // 输入节点数据 newNode->data = x; // 设置节点的数据 newNode->next = new Node; // 为下一个节点分配新内存 newNode = newNode->next; // 移动到下一个节点 newNode->next = NULL; // 将新节点的next设置为NULL } PrintNode(); // 打印链表 } // 在指定位置插入新节点的函数 void InsertNode(){ int position, data; // 临时变量position和data,用于存储插入位置和数据 cout << "请输入插入节点的位置和数据: "; cin >> position >> data; // 输入插入位置和数据 Node *p = head, *newNode; // 指针p用于遍历链表,指针newNode用于创建新节点 int j = 1; // 计数器j,用于遍历链表 if(position == 0){ // 在链表头部插入节点 newNode = new Node; newNode->data = data; newNode->next = p; head = newNode; } else if (position <= n + 1){ // 在链表中间或末尾插入节点 while (j <= position - 1){ p = p->next; // 移动到插入位置前一个节点 j++; } newNode = new Node; // 创建新节点 newNode->data = data; newNode->next = p->next; // 将新节点插入链表 p->next = newNode; n++; // 更新节点数量 } else { cout << "你输入的数字错误" << endl; } PrintNode(); // 打印更新后的链表 } // 从链表中删除节点的函数 void DeleteNode(){ int delete_position; // 临时变量delete_position,用于存储删除位置 cout << "请输入要删除的节点位置: "; cin >> delete_position; // 输入删除位置 Node *delete_node = head, *temp_delete_node; // 指针delete_node用于遍历链表,指针temp_delete_node用于临时存储节点 if (delete_position == 1){ // 删除头节点 head = head->next; // 更新头指针 delete delete_node; // 释放头节点的内存 } else { for (int i = 1; i < delete_position - 1; i++) { temp_delete_node = delete_node->next; // 移动到删除位置前一个节点 } temp_delete_node = delete_node->next; // 要删除的节点 delete_node->next = temp_delete_node->next; // 将节点从链表中移除 delete temp_delete_node; // 释放节点的内存 } n--; // 更新节点数量 PrintNode(); // 打印更新后的链表 } // 在链表中查找具有给定值的节点的函数 void SearchNode() { int search_value; // 临时变量search_value,用于存储查找值 cout << "请输入要查找的值: "; cin >> search_value; // 输入查找值 Node *current = head; // 指针current用于遍历链表 int position = 1; // 计数器position,用于记录节点位置 while (current != NULL) { if (current->data == search_value) { cout << "值 " << search_value << " 在位置 " << position << " 找到" << endl; return; // 如果找到值则退出函数 } current = current->next; // 移动到下一个节点 position++; // 更新位置 } cout << "值 " << search_value << " 在链表中未找到." << endl; } // 打印链表中所有节点的函数 void PrintNode(){ Node *link = head; // 指针link用于遍历链表 if (link == NULL){ cout << "链表为空." << endl; return; } cout << "节点的数据是: "; do { cout << link->data << " "; // 打印节点数据 link = link->next; // 移动到下一个节点 } while (link->next != NULL); cout << endl; } int main(){ AddNode(); // 调用函数添加节点 InsertNode(); // 调用函数插入节点 DeleteNode(); // 调用函数删除节点 SearchNode(); // 调用函数查找节点 return 0; } |
二、双向链表(Doubly Linked List )
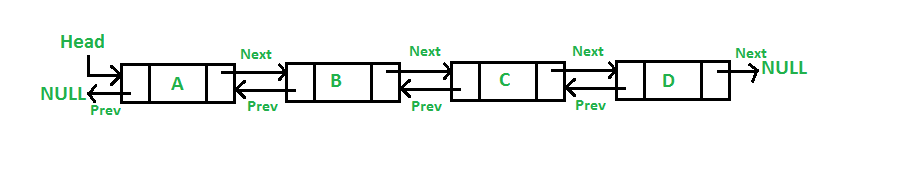
每个结点有两个指针域和若干数据域,其中一个指针域指向它的前趋结点,另一个指针域指向它的后继结点。它的优点是访问、删除、插入更方便,速度更快,但是以空间换时间。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 | /**************************************************************** * 代码作者: Alex Li * 创建时间: 2023-05-22 16:03:37 * 最后修改: 2025-01-10 22:11:00 * 文件描述: 双向链表(doubly linked list) ****************************************************************/ #include <iostream> using namespace std; // 节点结构定义 struct Node { int data; // 数据域 struct Node* next; // 指向下一个节点的指针 struct Node* prev; // 指向前一个节点的指针 }; struct Node* head = NULL; // 全局头节点,初始化为空 // 在链表的开头插入节点 void insertFront(int data) { // 分配新节点的内存 struct Node* newNode = new Node; // 将数据赋值给新节点 newNode->data = data; // 将新节点的 next 指向当前头节点 newNode->next = head; // 将新节点的 prev 指向空 newNode->prev = NULL; // 如果当前链表不为空,将原头节点的 prev 指向新节点 if (head != NULL) head->prev = newNode; // 更新头节点为新节点 head = newNode; } // 在指定节点之后插入新节点 void insertAfter(struct Node* prev_node, int data) { // 检查给定的前节点是否为空 if (prev_node == NULL) { cout << "前一个节点不能为空"; return; } // 分配新节点的内存 struct Node* newNode = new Node; // 将数据赋值给新节点 newNode->data = data; // 将新节点的 next 指向前节点的 next newNode->next = prev_node->next; // 将前节点的 next 指向新节点 prev_node->next = newNode; // 将新节点的 prev 指向前节点 newNode->prev = prev_node; // 如果新节点的 next 不为空,将其 next 节点的 prev 指向新节点 if (newNode->next != NULL) newNode->next->prev = newNode; } // 在链表末尾插入新节点 void insertEnd(int data) { // 分配新节点的内存 struct Node* newNode = new Node; // 将数据赋值给新节点 newNode->data = data; // 将新节点的 next 指向空 newNode->next = NULL; // 临时存储头节点,用于遍历链表 struct Node* temp = head; // 如果链表为空,将新节点作为头节点 if (head == NULL) { newNode->prev = NULL; head = newNode; return; } // 如果链表不为空,遍历到链表末尾 while (temp->next != NULL) temp = temp->next; // 将最后一个节点的 next 指向新节点 temp->next = newNode; // 将新节点的 prev 指向最后一个节点 newNode->prev = temp; } // 删除链表中的节点 void deleteNode(struct Node* del_node) { // 如果头节点或待删除节点为空,则无法删除 if (head == NULL || del_node == NULL) return; // 如果待删除节点是头节点,将头节点指向其下一个节点 if (head == del_node) head = del_node->next; // 如果待删除节点不是最后一个节点,将其下一个节点的 prev 指向其前一个节点 if (del_node->next != NULL) del_node->next->prev = del_node->prev; // 如果待删除节点不是第一个节点,将其前一个节点的 next 指向其下一个节点 if (del_node->prev != NULL) del_node->prev->next = del_node->next; // 释放待删除节点的内存 delete del_node; } // 打印链表中的所有节点 void displayList() { struct Node* last; last = head; while (last != NULL) { // 遍历链表并打印数据 cout << last->data << " "; last = last->next; } if (head == NULL) // 如果链表为空,打印 NULL cout << "NULL\n"; cout << endl; } int main() { // 初始化空链表并插入节点 insertEnd(5); insertFront(1); insertFront(6); insertEnd(9); // 在头节点后插入 11 insertAfter(head, 11); // 在第二个节点后插入 15 insertAfter(head->next, 15); // 删除链表中的节点 deleteNode(head->next->next->next->next); // 打印链表 displayList(); } |
三、循环链表(Circular Linked List )
1、单向循环链表(singly circular linked list )的最后一个结点的指针指向头结点。如图:

2、双向循环链表(doubly circular linked list) 它的每个数据结点中都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点。如图:

四、静态链表
用数组来表示链表,称为静态链表。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 | /**************************************************************** * Description: 静态链表,用过的结点要回收 * Author: Alex Li * Date: 2022-08-04 11:22:42 * LastEditTime: 2024-08-05 19:39:49 ****************************************************************/ #include <iostream> using namespace std; const int N = 100010; // 定义常量N,表示数组的最大长度 int n = 0; // 当前链表节点数 int node[N], node_next[N]; // 分别存储节点的值和下一个节点的下标 int head, idx; // 头节点下标和当前可用的节点下标 int free_list_head; // 空闲链表的头节点 // 初始化链表 void init(){ head = -1; // 初始头节点下标设为-1 idx = 0; // 初始可用节点下标设为0 free_list_head = -1; // 初始空闲链表头节点设为-1 } // 从空闲链表中获取一个空闲下标 int get_free_index() { if (free_list_head == -1) { return idx++; // 如果空闲链表为空,返回当前可用下标并自增 } else { int free_idx = free_list_head; // 获取空闲链表的头节点 free_list_head = node_next[free_list_head]; // 更新空闲链表头节点 return free_idx; // 返回空闲下标 } } // 将x插入到头节点上 void firstNode(int x){ int new_idx = get_free_index(); // 获取一个空闲下标 node[new_idx] = x; // 在该下标处插入节点值x node_next[new_idx] = head; // 当前节点的next指向之前的头节点 head = new_idx; // 更新头节点下标为当前节点下标 n++; // 节点数加1 } // 将x插入到下标为k的点的后面 void add(int k, int x){ int new_idx = get_free_index(); // 获取一个空闲下标 node[new_idx] = x; // 在该下标处插入节点值x node_next[new_idx] = node_next[k]; // 当前节点的next指向下标为k节点的下一个节点 node_next[k] = new_idx; // 更新下标为k节点的next指向当前节点下标 n++; // 节点数加1 } // 删除下标为k的节点的后一个节点 void remove(int k){ if (node_next[k] != -1) { // 确保k节点后面有节点 int remove_idx = node_next[k]; // 获取要删除节点的下标 node_next[k] = node_next[remove_idx]; // 更新k节点的next指向被删除节点的next node_next[remove_idx] = free_list_head; // 将被删除节点插入到空闲链表的头部 free_list_head = remove_idx; // 更新空闲链表头节点 n--; // 节点数减1 } } // 打印链表中的所有节点 void printNode(){ int i = head; // 从头节点开始 while (i != -1) { // 遍历链表直到末尾 cout << node[i] << " "; // 打印当前节点值 i = node_next[i]; // 移动到下一个节点 } cout << endl; } int main(){ int k, option, position, value; init(); // 初始化链表 do { cout << "请选择要执行的操作,输入选项编号:" << endl; cout << "0. 退出" << endl; cout << "1. 插入头节点" << endl; cout << "2. 插入新节点" << endl; cout << "3. 删除节点" << endl; cout << "4. 打印链表" << endl; cin >> option; // 输入选项编号 switch (option) { case 0: break; case 1: cout << "输入头节点的值:" << endl; cin >> value; firstNode(value); break; case 2: cout << "输入新节点的位置(插入到k后面)和值:" << endl; cin >> k >> value; add(k, value); break; case 3: cout << "输入要删除的节点位置:" << endl; cin >> k; remove(k); break; case 4: printNode(); break; default: cout << "请输入正确的选项编号" << endl; } } while (option != 0); return 0; } |
习题:小熊的果篮
题目描述
小熊的水果店里摆放着一排 nn个水果。每个水果只可能是苹果或桔子,从左到右依次用正整数 1,2,…,n 编号。连续排在一起的同一种水果称为一个“块”。小熊要把这一排水果挑到若干个果篮里,具体方法是:每次都把每一个“块”中最左边的水果同时挑出,组成一个果篮。重复这一操作,直至水果用完。注意,每次挑完一个果篮后,“块”可能会发生变化。比如两个苹果“块”之间的唯一桔子被挑走后,两个苹果“块”就变成了一个“块”。请帮小熊计算每个果篮里包含的水果。
输入格式
第一行,包含一个正整数 n,表示水果的数量。
第二行,包含 n 个空格分隔的整数,其中第 i 个数表示编号为 i 的水果的种类,1 代表苹果,0 代表桔子。
输出格式
输出若干行。
第 i 行表示第 i 次挑出的水果组成的果篮。从小到大排序输出该果篮中所有水果的编号,每两个编号之间用一个空格分隔。
输入输出样例
输入 #1
12 1 1 0 0 1 1 1 0 1 1 0 0
输出 1
1 3 5 8 9 11
2 4 6 12
7
10
输入 2
20
1 1 1 1 0 0 0 1 1 1 0 0 1 0 1 1 0 0 0 0
输出2
21 5 8 11 13 14 15 17
2 6 9 12 16 18
3 7 10 19
4 20
说明/提示
【样例解释 #1】
这是第一组数据的样例说明。
所有水果一开始的情况是 [1,1,0,0,1,1,1,0,1,1,0,0],一共有 6 个块。
在第一次挑水果组成果篮的过程中,编号为 1,3,5,8,9,11的水果被挑了出来。
之后剩下的水果是 [1,0,1,1,1,0],一共 4 个块。
在第二次挑水果组成果篮的过程中,编号为 2,4,6,12 的水果被挑了出来。
之后剩下的水果是 [1,1],只有 1 个块。
在第三次挑水果组成果篮的过程中,编号为 7 的水果被挑了出来。
最后剩下的水果是 [1],只有 1 个块。
在第四次挑水果组成果篮的过程中,编号为10 的水果被挑了出来。
【数据范围】
对于 10%10% 的数据,n≤5n≤5。
对于 30%30% 的数据,n≤1000n≤1000。
对于 70%70% 的数据,n≤50000n≤50000。
对于 100%100% 的数据,1≤n≤2×1051≤n≤2×105。
[2021CSP-J-4][洛谷P7912] [4973]
