归并排序(merge sort)
组别:提高级
难度:5
洛谷:P2804, P1309
归并排序是基于分治算法的一种排序,我们把一个问题分解成子问题,每个子问题再分别解决,最后再把子问题的解合并成最终结果。
如下图数列{6,5,12,10,9,1},首先将数列分成两分{6,5,12}和{10,9,1},再把这俩个子数列继续分解成{6},{5,12},{10},{9,1} ,当就子数列就剩两个元素时比较大小,现把子数列逐级合并成一个有序数列。

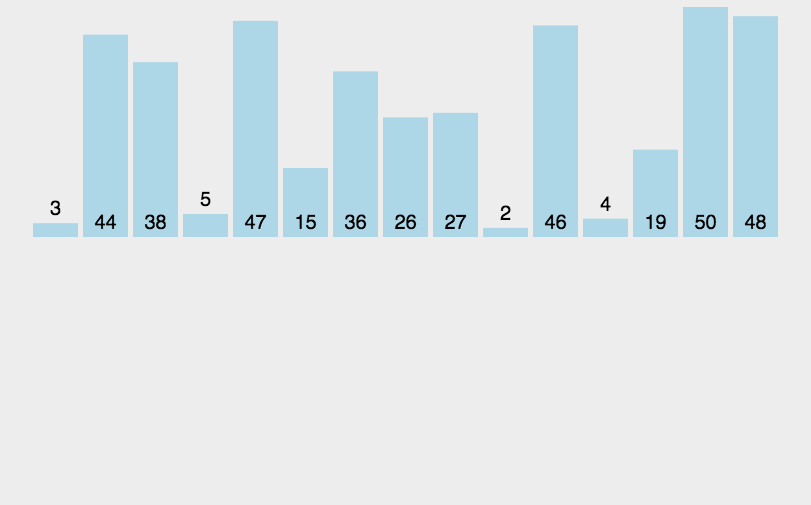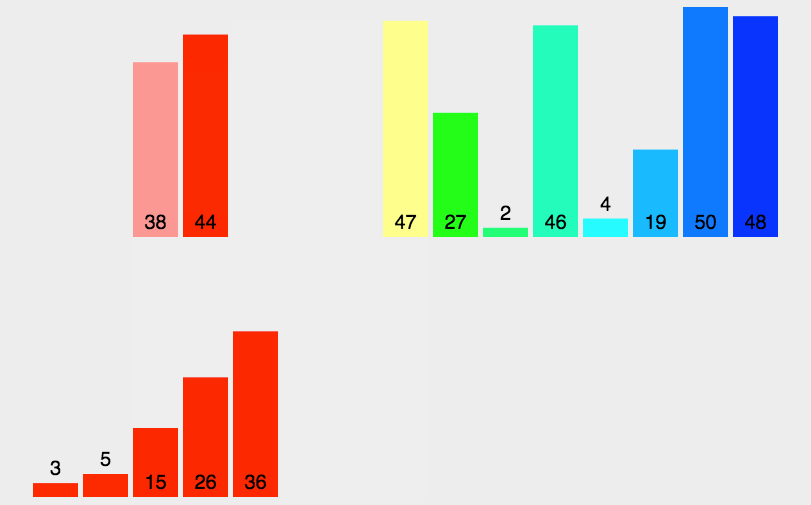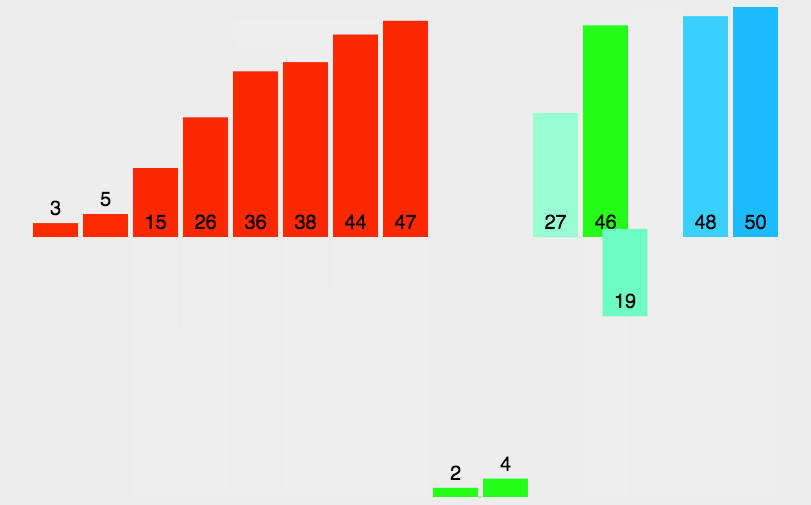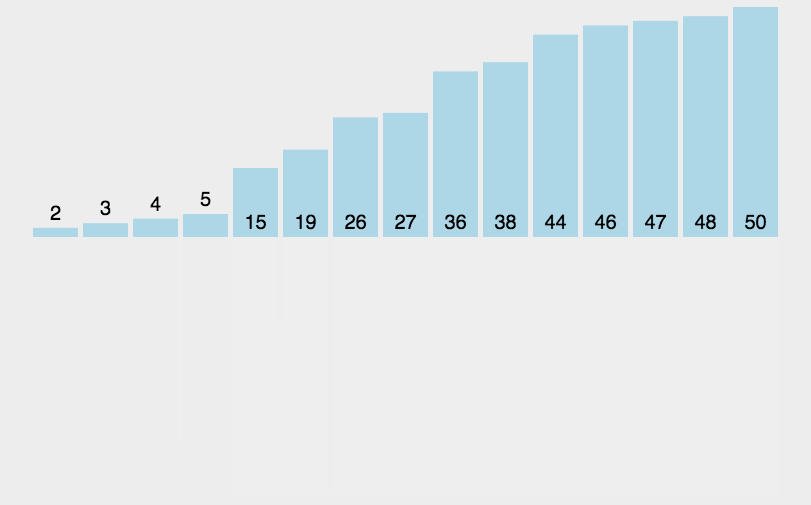
代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 | /**************************************************************** * 代码作者: Alex Li * 创建时间: 2022-07-27 12:52:48 * 最后修改: 2025-04-06 13:19:55 * 文件描述: 归并排序算法 ****************************************************************/ #include <iostream> #include <vector> using namespace std; void merg(vector<int> &arr,int l, int r){ int mid=l+(r-l)/2; vector<int> temp(r - l + 1); int i = l, j = mid + 1, k = 0; // 合并左右部分 while (i <= mid && j <= r) { if (arr[i] <= arr[j]) { temp[k++] = arr[i++]; } else { temp[k++] = arr[j++]; } } // 处理剩余元素 while (i <= mid) temp[k++] = arr[i++]; while (j <= r) temp[k++] = arr[j++]; // 将临时数组复制回原数组 for (k = 0; k < temp.size(); ++k) { arr[l + k] = temp[k]; } } /* arr 待排序的数组 l 左边界 r 右边界 */ void mergeSort(vector<int>& arr, int l, int r) { if (l >= r) return; // 如果区间长度为1或无效,直接返回 int mid = l + (r - l) / 2; // 计算中间位置,防止整型溢出 mergeSort(arr, l, mid); // 递归排序左半部分 mergeSort(arr, mid + 1, r); // 递归排序右半部分 merg(arr,l, r); } int main() { int size; cout << "请输入数组大小:"; cin >> size; if (size > 100) { cout << "数组大小超出限制!" << endl; return -1; } vector<int> arr(size); cout << "请输入" << size << "个元素:"; for (int i = 0; i < size; i++) cin >> arr[i]; mergeSort(arr, 0, size - 1); cout << "排序后的数组:"; for (int i = 0; i < size; i++) cout << arr[i] << " "; cout << endl; return 0; } |
逆序对问题:
要在 Merge Sort 基础上解决逆序对问题,可以通过在合并阶段计算出逆序对的数量。在逆序对问题中,如果在数组中 i < j 但是 arr[i] > arr[j],那么我们就称 (i, j) 是一个逆序对。
下面是一个基于 Merge Sort 的方法,通过在合并的过程中统计逆序对的数量来解决这个问题。
思路:
- 在每次合并子数组的过程中,如果左子数组的元素大于右子数组的元素,那么这些左子数组的元素与当前右子数组的元素构成逆序对,因为左子数组元素的索引比右子数组元素的索引小。
while (i <= mid && j <= r) { // 比较左右区间元素
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
inversion_count += (mid - i + 1); // 这些元素与 arr[j] 构成逆序对
}
}
