哈夫曼树

组别：入门级
难度：4
OJ平台：LQ1009

当我们想传递一个字符串”shannon”从一台电脑到另一台电脑，我们需要对”shannon”的第一个字符做编码，转换成二进制传输，在四种编码中，只有a->000, h->001, n->1 , o->011, s->010这个编码方式所需要传输的量最小，这就是哈夫曼编码，如何寻找合适的哈夫曼编码就构建哈夫曼树。

哈夫曼（David Albert Huffman, 1925年8月9日 – 1999年10月7日）是一位美国计算机科学家，因其发明的哈夫曼编码（Huffman Coding）而闻名于世。

WPL (Weighted Path Length, 带权路径长度)

定义：

在一棵树中，带权路径长度是指从根节点到所有叶子节点的路径长度与对应叶子节点权值的乘积之和。
公式为：WPL=\(\sum_{i=1}^{n}w_il_i\)

其中：
n 是叶子节点的数量。
w_i 是第 i个叶子节点的权值。
l_i是第 i 个叶子节点到根节点的路径长度。

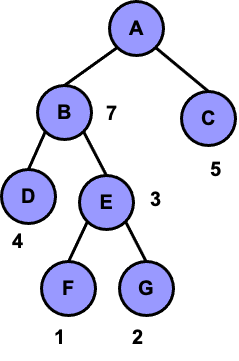
WPL=4*2+1*3+2*3+3*2+7*1+5*1=35

哈夫曼树

哈夫曼树又称最优二叉树，给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度(WPL)达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

例有4个结点，权值分别为7，5，2，4，构造有4个叶子结点的二叉树，第三个二叉树的WPL最小。要使二叉树WPL小,就须在构造树时, 将权值大的结点靠近根。

哈夫曼编码

哈夫曼编码是一种压缩编码的编码算法，是基于哈夫曼树的一种编码方式。哈夫曼树又称为带权路径长度最短的二叉树。

如何构建哈夫曼树及生成哈夫曼编码，是采用贪心策略。见图示。

注：哈夫曼树和哈夫曼编码不唯一，由于元素放左或放右的区别导致树的结构不同，但 WPL依然相同
N=2n-1, N为总结点数, n为叶子结点。

哈夫曼树

代码实现一：

/**************************************************************** 
 * 代码作者: Alex Li
 * 创建时间: 2025-01-11 20:20:05
 * 最后修改: 2025-01-11 23:59:24
 * 文件描述: 生成哈夫曼树
****************************************************************/
#include <iostream>
#include <queue>
using namespace std;

#define MAX_SIZE 100

// 定义哈夫曼树节点结构
struct HuffmanTreeNode{
    char data; // 节点存储的字符
    int freq;  // 节点存储的字符频率
    HuffmanTreeNode* left; // 左子节点
    HuffmanTreeNode* right; // 右子节点
};

// 定义比较器，用于优先队列中的节点比较
struct Compare{
    bool operator()(HuffmanTreeNode* a, HuffmanTreeNode* b){
        return a->freq > b->freq; // 频率较小的节点优先
    }
};

// 构造哈夫曼树的函数
HuffmanTreeNode* generateTree(priority_queue<HuffmanTreeNode*,vector<HuffmanTreeNode*>,Compare> &pq){
    // 当优先队列中只有一个节点时，生成结束
    while(pq.size() != 1){
        // 取出两个最小频率的节点
        HuffmanTreeNode* left = pq.top();
        pq.pop();
        HuffmanTreeNode* right = pq.top();
        pq.pop();

        // 创建新节点，频率为两个子节点频率之和
        HuffmanTreeNode* node = new HuffmanTreeNode;
        node->data = '$'; // 特殊字符表示内部节点
        node->freq = left->freq + right->freq;
        node->left = left;
        node->right = right;

        // 将新节点插入优先队列
        pq.push(node);
    }
    return pq.top(); // 返回根节点
}

// 打印哈夫曼编码的函数
void printCodes(HuffmanTreeNode* root, int arr[], int top){
    // 如果有左子节点，递归分配 0
    if(root->left){
        arr[top] = 0;
        printCodes(root->left, arr, top + 1);
    }

    // 如果有右子节点，递归分配 1
    if(root->right){
        arr[top] = 1;
        printCodes(root->right, arr, top + 1);
    }

    // 如果是叶子节点，打印字符及其编码
    if(!root->left && !root->right){
        cout << root->data << " ";
        for(int i = 0; i < top; i++){
           cout << arr[i];
        }
        cout << endl;
    }
}

// 删除哈夫曼树，释放内存
void deleteTree(HuffmanTreeNode* root) {
    if (!root) return;
    deleteTree(root->left);
    deleteTree(root->right);
    delete root;
}

// 生成哈夫曼树并打印编码的主函数
void HuffmanCodes(char data[], int freq[], int size){
    // 创建优先队列
    priority_queue<HuffmanTreeNode*, vector<HuffmanTreeNode*>, Compare> pq;

    // 将所有字符和频率插入优先队列
    for(int i = 0; i < size; i++){
        HuffmanTreeNode* newNode = new HuffmanTreeNode;
        newNode->data = data[i];
        newNode->freq = freq[i];
        pq.push(newNode);
    }

    // 生成哈夫曼树
    HuffmanTreeNode* root = generateTree(pq);

    // 打印哈夫曼编码
    int arr[MAX_SIZE], top = 0;
    printCodes(root, arr, top);

    // 删除树，释放内存
    deleteTree(root);
}

// 主函数
int main(){
    // 定义字符数组和对应的频率数组
    char data[] = {'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h'};
    int freq[] = {5, 29, 7, 8, 14, 23, 3, 11};
    int size = sizeof(data) / sizeof(data[0]); // 计算数组大小

    // 调用主函数生成哈夫曼编码
    HuffmanCodes(data, freq, size);

    return 0;
}

代码实现二：

/**************************************************************** 
 * 代码作者: Alex Li
 * 创建时间: 2025-01-11 20:20:05
 * 最后修改: 2025-01-12 00:19:08
 * 文件描述: 生成HuffmanTree, 用pair数据结构+构造函数
****************************************************************/
#include <iostream>
#include <queue>
using namespace std;

#define MAX_SIZE 100

struct HuffmanTreeNode{
    
        char data;
        int  freq;
        HuffmanTreeNode* left;
        HuffmanTreeNode* right;
     HuffmanTreeNode(char character,int frequency){
        data = character;
        freq = frequency;
        left = right = NULL;
    }
    
    
};

struct Compare{
        bool operator()(HuffmanTreeNode* a, HuffmanTreeNode* b){
              return a->freq>b->freq;
        }
};

HuffmanTreeNode* generateTree(priority_queue<HuffmanTreeNode*,vector<HuffmanTreeNode*>,Compare> &pq){
    
    while(pq.size()!=1){
        HuffmanTreeNode* left=pq.top();
        pq.pop();
        HuffmanTreeNode* right=pq.top();
        pq.pop();

        HuffmanTreeNode* node=new HuffmanTreeNode('$',left->freq+right->freq);
      
        node->left=left;
        node->right=right;
        pq.push(node);
    }
     return pq.top();
}

void printCodes(HuffmanTreeNode* root,int arr[],int top){
    if(root->left){
        arr[top]=0;
        printCodes(root->left,arr,top+1);
    }

    if(root->right){
        arr[top]=1;
        printCodes(root->right,arr, top+1);
    }

    if(!root->left && !root->right){
        cout<<root->data<<" ";
        for(int i=0;i<top;i++){
           cout<<arr[i];
        }
        cout<<endl;
    }
}

void deleteTree(HuffmanTreeNode* root) {
    if (!root) return;
    deleteTree(root->left);
    deleteTree(root->right);
    delete root;
}

void HuffmanCodes(vector<pair<char,int>>  HuffTree, int size){
    priority_queue<HuffmanTreeNode*,vector<HuffmanTreeNode*>,Compare> pq;

    for(int i=0; i<size;i++){
        HuffmanTreeNode* newNode=new HuffmanTreeNode(HuffTree[i].first,HuffTree[i].second);
   
        pq.push(newNode);
    }

    HuffmanTreeNode* root=generateTree(pq);

    int arr[MAX_SIZE],top=0;
    printCodes(root,arr,top);
    deleteTree(root);
}



int main(){
    
    vector<pair<char,int> >  HuffTree={
    {'a', 5},
    {'b', 29},
    {'c', 7},
    {'d', 8},
    {'e', 14},
    {'f', 23},
    {'g', 3},
    {'h', 11}
};
    
    HuffmanCodes(HuffTree,HuffTree.size());

  
    return 0;
}

LQ1009

LQ1009_1

Quizzes

小测验-哈夫曼树

Previous Topic

Back to Lesson

Next Quiz

数据结构与算法

哈夫曼树

WPL (Weighted Path Length, 带权路径长度)

哈夫曼树