回朔算法-N皇后问题

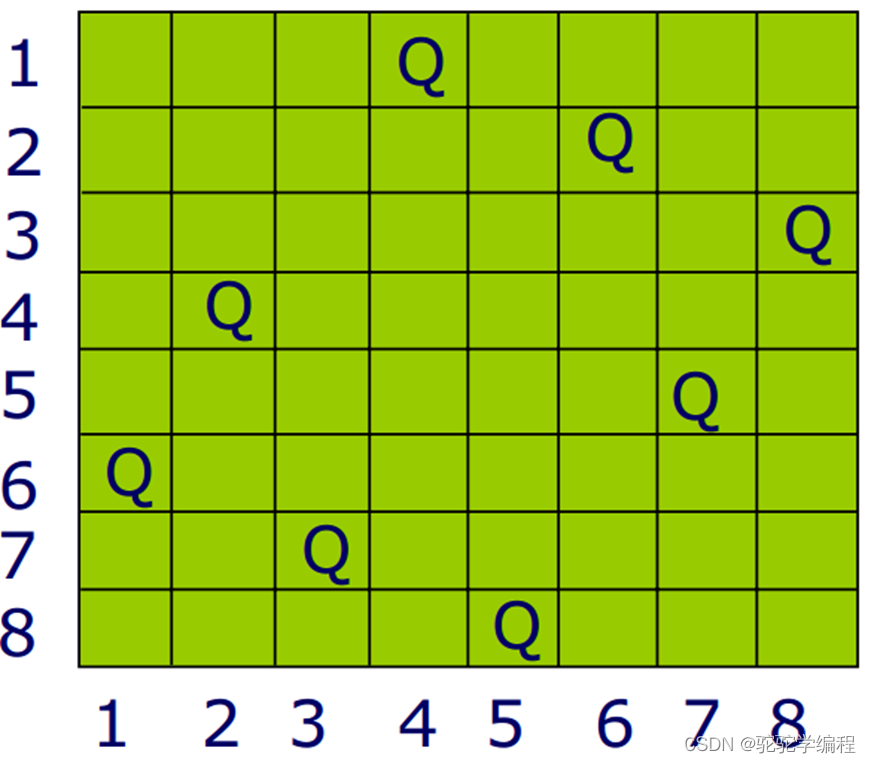
八皇后问题是十九世纪著名的数学家高斯于1850年提出的，并给出76组解。问题是:在8×8的棋盘上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上。用计算机计算，共有92组解。可以把八皇后问题扩展到n皇后问题，即在n×n的棋盘上摆放n个皇后，使任意两个皇后都不能处于同一行、同一列或同一斜线上。

N 皇后问题的解的数量随着 N 的增加而迅速增长。以下是前几项的解的数量：

N=1：1
N=2：0
N=3：0
N=4：2
N=5：10
N=6：4
N=7：40
N=8：92

代码说明

输入：
- 用户输入棋盘大小N。
核心逻辑：
- 使用递归与回溯法，在棋盘上尝试放置皇后。
- 每次放置皇后时，确保当前行、列和对角线无冲突。
- 如果成功放置 N 个皇后，记录解的数量并打印棋盘。
输出：
- 打印所有可能的解。
- 输出解的总数或提示无解。
时间复杂度： O(N!)

/**************************************************************** 
 * 代码作者: Alex Li
 * 创建时间: 2023-07-27 18:51:55
 * 最后修改: 2024-12-29 21:33:25
 * 文件描述: N皇后问题
****************************************************************/
#include <bits/stdc++.h>
using namespace std;

int N; // 棋盘大小
int counts = 0; // 解的数量，初始化为 0

/* 输出棋盘当前状态的工具函数 */
void printSolution(vector<vector<int>> &board) {
    for (int i = 0; i < N; i++) { // 遍历棋盘的每一行
        for (int k = 0; k < N; k++) { // 遍历棋盘的每一列
            cout << (board[i][k] ? "Q " : ". "); // 输出 "Q " 表示皇后，". " 表示空位
        }
        cout << "\n"; // 换行
    }
}

/* 检查在 board[row][column] 位置是否可以安全地放置皇后的工具函数 */
bool isSafe(vector<vector<int>> &board, int row, int column) {
    // 检查当前行左侧是否有皇后
    for (int i = 0; i < column; i++) {
        if (board[row][i]) return false; // 如果左侧存在皇后，返回 false
    }

    // 检查左上方对角线是否有皇后
    for (int i = row, j = column; i >= 0 && j >= 0; i--, j--) {
        if (board[i][j]) return false; // 如果左上方存在皇后，返回 false
    }

    // 检查左下方对角线是否有皇后
    for (int i = row, j = column; j >= 0 && i < N; i++, j--) {
        if (board[i][j]) return false; // 如果左下方存在皇后，返回 false
    }

    return true; // 如果没有威胁，返回 true
}

/* 递归函数：尝试在棋盘上放置皇后的工具函数 */
void solveNQUtil(vector<vector<int>> &board, int column) {
    // 基本条件：如果所有皇后都已成功放置，则增加解的数量并打印棋盘
    if (column >= N) {
        counts++; // 解的数量加一
        printSolution(board); // 打印当前解
        cout << '\n'; // 输出一个空行分隔解
        return; // 返回，继续寻找其他解
    }

    // 遍历当前列的所有行，尝试放置皇后
    for (int i = 0; i < N; i++) {
        // 检查当前行是否可以安全放置皇后
        if (isSafe(board, i, column)) {
            board[i][column] = 1; // 放置皇后
            solveNQUtil(board, column + 1); // 递归放置下一列的皇后
            board[i][column] = 0; // 回溯：移除当前皇后，尝试其他可能性
        }
    }
}

/* 主函数 */
int main() {
    cout << "Enter the size of the board (N): ";
    cin >> N; // 输入棋盘大小

    // 初始化棋盘，初始状态下所有格子均为 0（空）
    vector<vector<int>> board(N, vector<int>(N, 0));

    // 调用递归函数尝试放置皇后
    solveNQUtil(board, 0);

    // 根据解的数量输出结果
    if (counts > 0)
        cout << "There are " << counts << " solution.\n"; // 如果有解，输出解的数量
    else
        cout << "No solutions exist.\n"; // 如果没有解，输出提示

    return 0; // 程序结束
}

洛谷：P1562 P2105

Previous Topic

Back to Lesson

Next Topic

数据结构与算法

回朔算法-N皇后问题

代码说明