图的遍历(graph traversal)

数据结构与算法第五章图(gragh) 图的遍历(graph traversal)

一、图的遍历

从图中某一顶点出发系统地访问图中所有顶点，使每个顶点恰好被访问一次，这种运算操作被称为图的遍历。为了避免重复访问顶点，需要记录已访问过的顶点。
图的遍历分为深度优先遍历和广度优先遍历

二、深度优先遍历(DFS)

从图中某结点出发，访问其相邻结点(按编号最小或最大)，再访问该结点的相邻结点，直至访问完所有的结点。一条路走到头，回头再走没走过的路。可以看出DFS算法是一个递归的过程，其中需要借助一个栈完成操作。
基于邻接表的遍历的序列不唯一，基于邻接矩阵的遍历序列是唯一的。

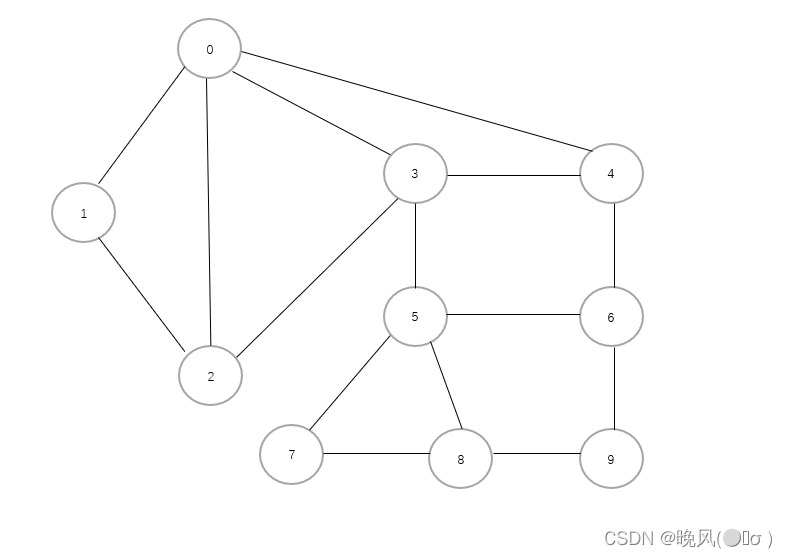
深度优先遍历(从大到小)：0，4，6，9，8，7，5，3，2，1。
深度优先遍历(从小到大)：0，1，2，3，4，6，5，7，8，9。

图的深度遍历-邻接表+递归

/**************************************************************** 
 * 代码作者: Alex Li
 * 创建时间: 2025-01-12 12:20:35
 * 最后修改: 2025-01-12 12:30:27
 * 文件描述: 图的深度遍历-邻接表+递归
****************************************************************/
#include <iostream>
#include <vector>

using namespace std;

void DFS(vector<vector<int>>& adjList, int vertex, vector<bool>& visited) {
    // 将当前顶点标记为已访问
    visited[vertex] = true;

    // 处理当前顶点
    cout << vertex << " ";

    // 递归访问所有未访问的邻接顶点
    for (int neighbor : adjList[vertex]) {
        if (!visited[neighbor]) {
            DFS(adjList, neighbor, visited);
        }
    }
}

int main() {
    // 创建一个有4个顶点和4条边的图的邻接表
    vector<vector<int>> adjList(4);
    adjList[0].push_back(1);
    adjList[1].push_back(0);
    adjList[1].push_back(2);
    adjList[2].push_back(1);
    adjList[2].push_back(3);
    adjList[3].push_back(2);

    // 创建一个布尔向量来跟踪访问状态
    vector<bool> visited(4, false);

    // 从顶点 0 开始执行深度优先搜索
    DFS(adjList, 0, visited);

    return 0;
}

图的深度遍历-邻接表+栈

/**************************************************************** 
 * 代码作者: Alex Li
 * 创建时间: 2025-01-12 12:33:40
 * 最后修改: 2025-01-12 12:43:19
 * 文件描述: 图的深度搜索-邻接表+栈
****************************************************************/
#include <iostream>
#include <vector>
#include <stack>

using namespace std;

void DFS(vector<vector<int>>& adjList, int startVertex) {
    // 创建一个布尔向量，用于跟踪是否访问过顶点
    vector<bool> visited(adjList.size(), false);
    // 使用显式栈保存顶点，用于模拟递归调用的行为
    stack<int> s;

    // 将起始顶点入栈
    s.push(startVertex);

    while (!s.empty()) {
        // 取出栈顶元素
        int vertex = s.top();
        s.pop();

        // 如果顶点还未被访问，处理它并标记为已访问
        if (!visited[vertex]) {
            cout << vertex << " ";  // 处理当前顶点
            visited[vertex] = true;
        }

        // 将所有未访问的邻接顶点入栈
        for (int neighbor : adjList[vertex]) {
            if (!visited[neighbor]) {
                s.push(neighbor);
            }
        }
    }
}

int main() {
    // 创建一个有4个顶点和4条边的图的邻接表
    vector<vector<int>> adjList(4);
    adjList[0].push_back(1);
    adjList[1].push_back(0);
    adjList[1].push_back(2);
    adjList[2].push_back(1);
    adjList[2].push_back(3);
    adjList[3].push_back(2);

    // 从顶点0开始执行深度优先搜索
    DFS(adjList, 0);
    return 0;
}

递归和显式栈的比较

特点	递归实现	显式栈实现
代码简洁性	更简洁，逻辑直接	需要手动管理栈，代码稍显复杂
函数调用栈	利用函数调用栈	使用显式栈替代函数调用栈
栈溢出问题	如果递归深度过大，可能导致栈溢出	不依赖函数栈，避免溢出问题
适用场景	图较小，递归深度有限	图较大，递归深度可能超过限制

五、图的深度遍历-邻接矩阵+栈

/**************************************************************** 
 * 代码作者: Alex Li
 * 创建时间: 2025-01-12 12:48:24
 * 最后修改: 2025-01-12 12:48:54
 * 文件描述: 图的深度搜索   邻接矩阵+栈
****************************************************************/
#include <iostream>
#include <vector>
#include <stack>

using namespace std;

void DFS(vector<vector<int>>& matrix, int startVertex) {
    int n = matrix.size(); // 顶点个数
    vector<bool> visited(n, false); // 标记访问状态
    stack<int> s; // 显式栈

    // 将起始顶点压入栈
    s.push(startVertex);

    while (!s.empty()) {
        // 获取栈顶元素
        int vertex = s.top();
        s.pop();

        // 如果当前顶点未被访问，则处理它
        if (!visited[vertex]) {
            cout << vertex << " "; // 处理当前顶点
            visited[vertex] = true; // 标记为已访问
        }

        // 遍历邻接矩阵中当前顶点的所有邻居
        // 注意要从高到低遍历，保证栈的深度优先顺序
        for (int i = n - 1; i >= 0; --i) {
            if (matrix[vertex][i] == 1 && !visited[i]) {
                s.push(i); // 将未访问的邻居压入栈
            }
        }
    }
}

int main() {
    // 定义一个4个顶点的图（邻接矩阵表示）
    vector<vector<int>> matrix = {
        {0, 1, 0, 0}, // 顶点 0
        {1, 0, 1, 0}, // 顶点 1
        {0, 1, 0, 1}, // 顶点 2
        {0, 0, 1, 0}  // 顶点 3
    };

    // 从顶点 0 开始深度优先遍历
    cout << "DFS Traversal: ";
    DFS(matrix, 0);

    return 0;
}

三、广度优先遍历(BFS)

图的广度遍历-邻接表+队列

/**************************************************************** 
 * 代码作者: Alex Li
 * 创建时间: 2025-01-12 13:04:08
 * 最后修改: 2025-01-12 13:05:17
 * 文件描述: 图的BFS，邻接表+队列
****************************************************************/
#include <iostream>
#include <queue>
#include <vector>

using namespace std;

const int MAX_VERTICES = 1000;

void BFS(vector<int>* adjList, int numVertices, int startVertex) {
    // 创建一个数组用于记录哪些顶点已经被访问
    bool visited[MAX_VERTICES] = { false };
    // 创建一个队列用于存储待处理的顶点
    queue<int> q;
    // 将起始顶点标记为已访问并加入队列
    visited[startVertex] = true;
    q.push(startVertex);
    // 开始处理队列中的顶点
    while (!q.empty()) {
        // 从队列中取出下一个顶点
        int vertex = q.front();
        q.pop();
        // 处理当前顶点
        cout << vertex << " ";
        // 将当前顶点所有未访问的邻居加入队列
        for (int i = 0; i < adjList[vertex].size(); ++i) {
            int neighbor = adjList[vertex][i];
            if (!visited[neighbor]) {
                visited[neighbor] = true; // 标记邻居为已访问
                q.push(neighbor);         // 将邻居加入队列
            }
        }
    }
}

int main() {
    // 创建一个有4个顶点和4条边的图的邻接表
    int numVertices = 4;
    vector<int> adjList[MAX_VERTICES];
    adjList[0].push_back(1); // 顶点0连接顶点1
    adjList[1].push_back(0); // 顶点1连接顶点0
    adjList[1].push_back(2); // 顶点1连接顶点2
    adjList[2].push_back(1); // 顶点2连接顶点1
    adjList[2].push_back(3); // 顶点2连接顶点3
    adjList[3].push_back(2); // 顶点3连接顶点2
    // 从顶点0开始执行广度优先搜索
    BFS(adjList, numVertices, 0);
    return 0;
}

图的广度遍历-邻接矩阵+队列

/**************************************************************** 
 * 代码作者: Alex Li
 * 创建时间: 2025-01-12 13:07:43
 * 最后修改: 2025-01-12 13:07:47
 * 文件描述: 图的广度优先搜索   邻接矩阵+队列
****************************************************************/
#include <iostream>
#include <queue>

using namespace std;

const int MAX_VERTICES = 1000;

void BFS(int adjMatrix[][MAX_VERTICES], int numVertices, int startVertex) {
    // 创建一个数组用于记录哪些顶点已经被访问
    bool visited[MAX_VERTICES] = { false };
    // 创建一个队列用于存储待处理的顶点
    queue<int> q;
    // 将起始顶点标记为已访问，并将其加入队列
    visited[startVertex] = true;
    q.push(startVertex);
    // 开始处理队列中的顶点
    while (!q.empty()) {
        // 从队列中取出下一个顶点
        int vertex = q.front();
        q.pop();
        // 处理当前顶点
        cout << vertex << " ";
        // 将当前顶点的所有未访问邻居加入队列
        for (int i = 0; i < numVertices; ++i) {
            if (adjMatrix[vertex][i] == 1 && !visited[i]) {
                visited[i] = true; // 标记邻居为已访问
                q.push(i);         // 将邻居加入队列
            }
        }
    }
}

int main() {
    // 创建一个有4个顶点和4条边的图的邻接矩阵
    int numVertices = 4;
    int adjMatrix[MAX_VERTICES][MAX_VERTICES] = {
         { 0, 1, 0, 0 }, // 顶点 0 的邻接情况
         { 1, 0, 1, 0 }, // 顶点 1 的邻接情况
         { 0, 1, 0, 1 }, // 顶点 2 的邻接情况
         { 0, 0, 1, 0 }  // 顶点 3 的邻接情况
       };
    // 从顶点0开始执行广度优先搜索
    BFS(adjMatrix, numVertices, 0);
    return 0;
}

B3862

B3862_1

B3862_2

P1294高手去散步

Previous Topic

Back to Lesson

Next Topic